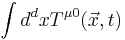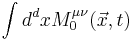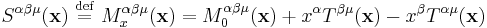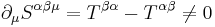Spin tensor

In mathematics and mathematical physics, the Euclidean group

SE(d)

of direct isometries is generated by translations and rotations. Its Lie algebra is written

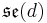\mathfrak{se}(d).

Contents

Noether currents

The Noether currents for the translations make up the stress-energy tensor 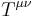T^{\mu\nu} \,.

It satisfies the continuity equation

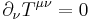\partial_\nu T^{\mu\nu}=0.

And

\int d^dx T^{\mu 0}(\vec{x},t)

gives the energy-momentum 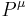P^\mu \, at time t, which is time-independent.

The Noether current for a rotation about the point y is given by 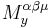M^{\alpha\beta\mu}_y.

Because of the Lie algebra relations,

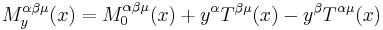M^{\alpha\beta\mu}_y(x)=M^{\alpha\beta\mu}_0(x)%2By^\alpha T^{\beta\mu}(x)-y^\beta T^{\alpha\mu}(x),

where 0 is the origin.

And

\int d^dx M^{\mu\nu}_0(\vec{x},t)

gives the angular momentum 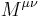M^{\mu\nu} \, at time t.

Definition

Define the spin tensor at a point 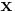\mathbf{x} to be the value of the Noether current at 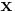\mathbf{x} of a rotation about x,

S^{\alpha\beta\mu}(\mathbf{x})\ \stackrel{\mathrm{def}}{=}\ M^{\alpha\beta\mu}_x(\mathbf{x})=M^{\alpha\beta\mu}_0(\mathbf{x})%2Bx^\alpha T^{\beta\mu}(\mathbf{x})-x^\beta T^{\alpha\mu}(\mathbf{x})

Because of the continuity equation

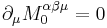\partial_\mu M^{\alpha\beta\mu}_0=0,

we get

\partial_\mu S^{\alpha\beta\mu}=T^{\beta\alpha}-T^{\alpha\beta} \neq 0

and therefore, the stress-energy tensor isn't symmetric.

S gives the spin density and M gives the angular momentum density. The angular momentum is the sum of the orbital angular momentum and spin.

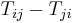T_{ij} - T_{ji} gives the torque density showing the rate of conversion between the orbital angular momentum and spin.

Examples

Examples of materials with a nonzero spin density are molecular fluids, the electromagnetic field and turbulent fluids. For molecular fluids, the individual molecules may be spinning. The electromagnetic field can have circularly polarized light. For turbulent fluids, we may arbitrarily make a distinction between long wavelength phenomena and short wavelength phenomena. A long wavelength vorticity may be converted via turbulence into tinier and tinier vortices transporting the angular momentum into smaller and smaller wavelengths while simultaneously reducing the vorticity. This can be approximated by the eddy viscosity.

See also